Dentre os polígonos de ouro estão o triângulo, o retângulo.
RETÂNGULO DE OURO
Os retângulos áureos estão nas obras gregas, nas obras de Leonardo da Vinci, Albrescht Dürer, Salvador Dali, dentre outros e também, em muitas obras da arquitetura clássica em que temos como exemplo claro o Pathernon.
Da Vinci
Leonardo da Vinci usou Phi para pintar a Mona Lisa, uma de suas mais notáveis obras. Em vários pontos da obra, tais como nas relações entre seu tronco e cabeça, ou entre os elementos do rosto aparece a razão áurea.

Outra obra de Da Vinci em que se vê com bastante clareza o uso da Razão Áurea é o Homem Vitruviano como nota-se na imagem a seguir.

Pathernon

Retângulo áureo no Parthenon
Na imagem abaixo, o frontispício dessa obra, hoje em ruínas, está sobreposta por formas retangulares.

Se dividirmos as medidas dos lados maiores pelas medidas dos lados menores desses retângulos, obteremos números próximos da razão a "phi" = 1,618034...
Chamamos de retângulo áureo aquele em que se aplica a seguinte propriedade: de um retângulo ABCD, suprimimos um quadrado ABEF, restando assim, um novo retângulo CDEF, sendo que, se este for semelhante ao original, então ABCD é áureo.
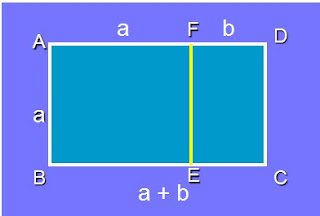
Assim, podemos traduzir a definição acima da seguinte maneira:
a/a+b = b/a (1)
Da relação (1) decorre, a seguinte propriedade das proporções, onde:

Isto significa que se o retângulo de lados a + b e a é áureo, logo o retângulo de lados a e b também será áureo e assim, sucessivamente.

Outras Aplicações
Ainda hoje há artistas usando a “divina proporção” em seus trabalhos, e cientistas, como Roger Penrose, estão descobrindo muitas aplicações da razão áurea na matemática e na natureza.
Sabe-se hoje que existe uma ligação entre a razão áurea e a série de Fibonacci. A seqüência 1, 1, 2, 3, 5, 8, 13, ..., correspondente aos lados dos quadrados que montam essa espiral, é a mesma que Leonardo Pisano (Fibonacci 1180-1250), em seu livro Liber Abbaci, de 1202, calculou para o crescimento das populações de coelhos a partir de um casal.
Dividindo, a partir do terceiro termo dessa seqüência, o número deste termo pelo número do termo anterior, teremos a seqüência de frações 1/1, 2/1, 3/2, 5/3, 8/5, 13/8, 21/13... que se aproximará cada vez mais da razão áurea fhi = 1,618034...
Observe a figura abaixo:

Assim, podemos perceber que razão entre os termos consecutivos da seqüência de Fibonacci tendem a phi.
A razão áurea e a seqüência de Fibonacci
Agrupados na forma vista na figura anterior, temos uma seqüência de quadrados com lados de medidas iguais aos números da seqüência de Fibonacci (1, 1, 2, 3, 5, 8, 13, 21...) e assim, se formará uma espiral muito encontrada em formas da natureza, a chamada Espiral de conchas e flores.

Esta espiral pode ser vista facilmente no molusco náutilo (Nautilus pompilius) e na distribuição de pétalas de diversas flores.

Observe na figura a seguir como realmente pode-se encontrar uma seqüência de retângulo de ouro formando a espiral de fibonacci.

TRIÂNGULO DE OURO
Um triângulo é um triângulo áureo quando ele é semelhante ao triângulo retângulo com hipotenusa medindo 1,618... (phi) e catetos com medidas 1 e 1,272... (raiz quadrada de phi). Assim, um triângulo retângulo com hipotenusa a e catetos b e c (b > c) é áureo se, e somente se,

Acredita-se que, no Egito, as pirâmides de Gizé foram construídas tendo em conta a razão áurea. A razão entre a altura de um face e metade do lado da base da grande pirâmide é igual ao número de ouro. O Papiro de Rhind (Egípcio) refere-se a uma “razão sagrada” que se crê ser o número de ouro. Esta razão ou secção áurea surge em muitas estátuas da antiguidade. A razão aparece, também, na proporção entre altura e lados e nas câmaras internas.


Logo, para verificarmos se uma pirâmide é ou não áurea, devemos analisar a seguinte definição:
Pirâmide reta de altura h com base quadrada de lado a e a altura de suas faces seja H. Desta maneira, quando o triângulo de lados H, h e a/2 for um triângulo áureo, a pirâmide também será áurea.
De acordo com a definição, tem-se:

Demonstração:
Uma pirâmide áurea, isto é, em que o triângulo retângulo com hipotenusa e catetos h e a/2, (supondo h > a/2) é áureo.
Temos então:

E portanto,

Analogamente, das relações, temos:

obtemos

que implica

que resulta

Logo,

e, portanto, o triângulo de lados H, h e a/2.
Muito interessante! O site está de parabéns!
ResponderExcluirMuito obrigado! Isso me motiva muito a tentar fazê-lo cada vez melhor. Abraço.
ExcluirNOSS CARA MUITO BOM VLW MESMO ME AJUDO E MUITO COM MEU TRABALHO DE MATEMATICA VLW ATE + ^^
ResponderExcluirÉ muito bom saber que este artigo lhe foi útil. Volte mais vezes. Um abraço.
Excluir