Um Quociente apaixonou-se
Um dia
Doidamente
Por uma Incógnita.
Olhou-a com seu olhar inumerável
E viu-a, do Ápice à Base...
Uma Figura Ímpar;
Olhos rombóides, boca trapezóide,
Corpo ortogonal, seios esferóides.
Fez da sua
Uma vida
Paralela à dela
Até que se encontraram
No Infinito.
"Quem és tu?" indagou ele
Com ânsia radical.
"Sou a soma do quadrado dos catetos.
Mas pode chamar-me "Hipotenusa."
E de falarem descobriram que eram
O que, em aritmética, corresponde
A alma irmãs
Primos-entre-si.
E assim se amaram
Ao quadrado da velocidade da luz.
Numa sexta potenciação
Traçando
Ao sabor do momento
E da paixão
Rectas, curvas, círculos e linhas sinusoidais.
Escandalizaram os ortodoxos
das fórmulas euclidianas
E os exegetas do Universo Finito.
Romperam convenções newtonianas e pitagóricas.
E, enfim, resolveram casar-se.
Constituir um lar.
Mais que um lar.
Uma Perpendicular.
Convidaram para padrinhos
O Poliedro e a Bissectriz.
E fizeram planos, equações e
diagramas para o futuro
Sonhando com uma felicidade
Integral
E diferencial.
E casaram-se e tiveram
uma secante e três cones
Muito engraçadinhos.
E foram felizes
Até àquele dia
Em que tudo, afinal,
se torna monotonia.
Foi então que surgiu
O Máximo Divisor Comum...
Frequentador de Círculos Concêntricos.
Viciosos.
Ofereceu-lhe, a ela,
Uma Grandeza Absoluta,
E reduziu-a a um Denominador Comum.
Ele, Quociente, percebeu
Que com ela não formava mais Um Todo.
Uma Unidade.
Era o Triângulo,
chamado amoroso.
E desse problema ela era a fracção
Mais ordinária.
Mas foi então que Einstein descobriu a Relatividade.
E tudo que era espúrio passou a ser
Moralidade
Como aliás, em qualquer
Sociedade
Millôr Fernandes
Caros amigos e visitantes, pretendo ao criar este blog, disponibilizar um espaço propício à reflexão sobre diversos tópicos e temas relacionados à Matemática em seus mais diversos ramos e possibilidades. Nele poderemos interagir e propor atividades, situações e tarefas susceptíveis que poderão, porque não, serem levadas à sala de aula, como jogos, aplicações, quebra-cabeças, enigmas, curiosidades, histórias dos diversos ramos da matemática etc.
quinta-feira, 25 de fevereiro de 2010
terça-feira, 23 de fevereiro de 2010
A ótica da visão humana
Ilusões de ótica
Olhe bem a figura a seguir e leia a frase escrita.

Observe a imagem a seguir.

Observe as situações a seguir.
Nas figuras a seguir, qual dos segmentos verticais tem o maior tamanho?

Essa é fácil hein... mas vamos lá, analise com calma e atenção.
A resposta é nenhum deles... ambos possuem o mesmo tamanho.

Na figura a seguir, o que você vê: uma espiral ou círculos concêntricos?


Pense bem... não quer pensar mais um pouco???
Pois bem, acredite ou não a figura central é um circulo perfeito.
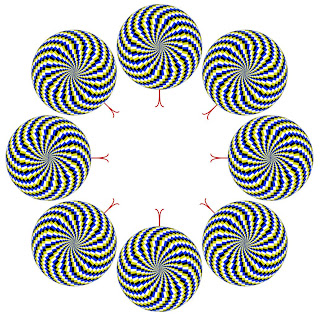
E nas três próximas imagens, em que sentido estão girando???


Olhe bem a figura a seguir e leia a frase escrita.

A frase lida por você é NÃO PARE NA PISTA??? Se a resposta for sim, acho melhor dar mais uma olhadinha. E agora, percebeu alguma diferença nessa frase?
Muitas pessoas precisam olhar várias vezes para perceber onde está o erro. Mas se você precisou olhar várias vezes, fique calmo. Isto é um fenômeno relacionado a uma prática bastante comum de vermos padrões de maneira global, sem nos atermos aos detalhes.
Em psicologia isto é chamado de Gestalt, ou seja, é uma teoria que considera os fenômenos psicológicos como um conjunto autônomo, indivisível e articulado na sua configuração, organização e lei interna.
Analisemos então, outras situações interessantes.
Observe a imagem a seguir.

Nesta imagem, as linhas horizontais são ou não são paralelas?
Por mais ilógico que pareça, todas as linhas horizontais desta figura são paralelas, mesmo quando há um deslocamento do padrão. Uma explicação bastante para essa ilusão se refere ao fato de que existem células no cortex visual que se encarregam de interpretar a linearidade de linhas contínuas. Quando alguma coisa nos chama a atenção, nossos olhos, o foco faz um processo de entrada e saída dessas linhas. Assim, no exemplo visto nesta imagem, quem desvia a atenção de nossos olhos é o movimento dos padrões. Logo, temos uma sensação descontinuidade e vemos as linhas oscilarem.
Observe as situações a seguir.
Nas figuras a seguir, qual dos segmentos verticais tem o maior tamanho?

Essa é fácil hein... mas vamos lá, analise com calma e atenção.
A resposta é nenhum deles... ambos possuem o mesmo tamanho.
Agora, em relação a imagem abaixo, temos que as figuras internas são as mesmas. Assim, como se explica o quadrado branco que aparece no segundo polígono?

O fato é que os triângulos verde e vermelho, possuem ângulos internos agudos com medidas diferentes, logo o seguimento formado por suas hipotenusas não estão alinhados. Logo, as figuras formadas não são triângulos (a primeira, por mais estranho que possa parecer é um quadrilátero) e muito menos polígonos semelhantes.
Na figura a seguir, o que você vê: uma espiral ou círculos concêntricos?

A imagem anterior, por incrível que pareça, apresentam curvas que são círculos concêntricos. Uma maneira simples para perceber a veracidade desta informação, seria acompanhar qualquer uma delas com a ponta de um lápis.
Uma teoria que poderia explicar este fenômeno, nos diz que este tipo “confusão” que temos ao olharmos a imagem, depende dos movimentos involuntários dos músculos ciliares, associados à confusão intencionalmente criada pelo fundo da imagem.
Vejamos outros exemplos
A figura central é um circulo perfeito ou não??

Pense bem... não quer pensar mais um pouco???
Pois bem, acredite ou não a figura central é um circulo perfeito.
E nas três próximas imagens, em que sentido estão girando???



Pois bem, não estão girando em nenhum sentido. Não há figura alguma que esteja girando dentre elas.
Poema Matemático
"Pra que dividir sem racionar
Na vida é sempre bom multiplicar
E por A mais B
Eu quero demonstrar
Que gosto imensamente de você
Por uma fração infinitesimal
Você criou um caso de cálculo integral
E para resolver este problema
Eu tenho um teorema banal
Quando dois meios se encontram desaparece a fração
E se achamos a unidade
Está resolvida a questão
Para finalizar vamos recordar
Que menos por menos dá mais, amor
Se vão as paralelas
Ao infinito se encontrar
Por que demoram tanto dois corações se integrar
Se desesperadamente, incomensuravelmente
Eu estou perdidamente apaixonado por você"
Antônio Carlos Jobim
Na vida é sempre bom multiplicar
E por A mais B
Eu quero demonstrar
Que gosto imensamente de você
Por uma fração infinitesimal
Você criou um caso de cálculo integral
E para resolver este problema
Eu tenho um teorema banal
Quando dois meios se encontram desaparece a fração
E se achamos a unidade
Está resolvida a questão
Para finalizar vamos recordar
Que menos por menos dá mais, amor
Se vão as paralelas
Ao infinito se encontrar
Por que demoram tanto dois corações se integrar
Se desesperadamente, incomensuravelmente
Eu estou perdidamente apaixonado por você"
Antônio Carlos Jobim
Pentagrama
As aplicações da relação de ouro na Matemática são inumeráveis. Podemos citar, além daquelas já vistas, o pentagrama.
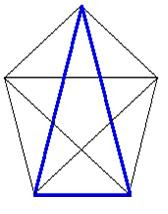

No primeiro pentagrama observamos que o triângulo possui seus lados em relação dourada com a base, enquanto o segundo triângulo possui sua base em relação dourada com os lados.
O pentagrama é uma das construções geométricas que mais fascinou os estudiosos em todos os tempos. Há uma inumerável quantidade de relações douradas dentro do pentagrama.
Leonardo da Vinci também utilizou-o para realizar algumas de suas mais famosas obras.
O Homem Vitruviano

Salvador Dali também fez uso da proporção áurea na tela Leda Atômica

Além de todos os exemplos que vimos a respeito das aplicações do número de ouro, temos ainda uma série de outras situações, sejam elas naturais ou criadas pelo homem, em que, a Divina Proporção se faz presente. As relações áureas também estão por toda a parte. Quando analisamos a configuração de animais e plantas, veremos muitos exemplos da existência de "phi".
Basta procuramos atentamente e a encontraremos em toda parte. A Razão Áurea foi muito importante no desenvolvimento da humanidade, seja nas construções, nas observações da Natureza ou na procura pela perfeição e/ou pelo belo. O Número de Ouro (phi) está sempre presente.
Agora, cabe àqueles que tenham se interessado por este assunto,definirem seus conceitos sobre harmonia, perfeição e beleza. E, por quê também não, buscar outros exemplos, outras aplicações. Este é um amplo, intrigante e revelador tema da matemática. E deixo uma diga para quem gosta de cinema: veja o filme O Código da Vinci. Não desconsiderando-se o fato de ser uma obra de ficção, em muitos momentos aborda-se este rico e magnífico tema.
Espero que tenham gostado. Abraços
Trabalho apresentado no XII Congresso de Educadores do Triângulo Mineiro
Autor:
SILVA, João Gilberto. O número de ouro e suas aplicações
REFERÊNCIAS BIBLIOGRÁFICAS
BOYER, Carl Benjamin. História da Matemática, tradução:
Elza Gomide. São Paulo. Edgard Blucher, 1974.
OSSERMAN, R. A Magia dos Números no Universo.
Editora Mercúrio Ltda. São Paulo. 1997
BIEMBENGUT, Maria Salett. Número de Ouro e Secção Áurea.
Editora da FURB, Blumenal, 1996.
HUNTLEY, H.E., A divina proporção : um ensaio sobre a beleza na matemática.
Editora: Universidade de Brasilia,1985


No primeiro pentagrama observamos que o triângulo possui seus lados em relação dourada com a base, enquanto o segundo triângulo possui sua base em relação dourada com os lados.
O pentagrama é uma das construções geométricas que mais fascinou os estudiosos em todos os tempos. Há uma inumerável quantidade de relações douradas dentro do pentagrama.
Leonardo da Vinci também utilizou-o para realizar algumas de suas mais famosas obras.
O Homem Vitruviano

Salvador Dali também fez uso da proporção áurea na tela Leda Atômica

Além de todos os exemplos que vimos a respeito das aplicações do número de ouro, temos ainda uma série de outras situações, sejam elas naturais ou criadas pelo homem, em que, a Divina Proporção se faz presente. As relações áureas também estão por toda a parte. Quando analisamos a configuração de animais e plantas, veremos muitos exemplos da existência de "phi".
Basta procuramos atentamente e a encontraremos em toda parte. A Razão Áurea foi muito importante no desenvolvimento da humanidade, seja nas construções, nas observações da Natureza ou na procura pela perfeição e/ou pelo belo. O Número de Ouro (phi) está sempre presente.
Agora, cabe àqueles que tenham se interessado por este assunto,definirem seus conceitos sobre harmonia, perfeição e beleza. E, por quê também não, buscar outros exemplos, outras aplicações. Este é um amplo, intrigante e revelador tema da matemática. E deixo uma diga para quem gosta de cinema: veja o filme O Código da Vinci. Não desconsiderando-se o fato de ser uma obra de ficção, em muitos momentos aborda-se este rico e magnífico tema.
Espero que tenham gostado. Abraços
Trabalho apresentado no XII Congresso de Educadores do Triângulo Mineiro
Autor:
SILVA, João Gilberto. O número de ouro e suas aplicações
REFERÊNCIAS BIBLIOGRÁFICAS
BOYER, Carl Benjamin. História da Matemática, tradução:
Elza Gomide. São Paulo. Edgard Blucher, 1974.
OSSERMAN, R. A Magia dos Números no Universo.
Editora Mercúrio Ltda. São Paulo. 1997
BIEMBENGUT, Maria Salett. Número de Ouro e Secção Áurea.
Editora da FURB, Blumenal, 1996.
HUNTLEY, H.E., A divina proporção : um ensaio sobre a beleza na matemática.
Editora: Universidade de Brasilia,1985
segunda-feira, 22 de fevereiro de 2010
Polígonos de Ouro
A “lei da divina proporção” está presente em diversas figuras planas, sólidos geométricos e na natureza.
Dentre os polígonos de ouro estão o triângulo, o retângulo.
RETÂNGULO DE OURO
Os retângulos áureos estão nas obras gregas, nas obras de Leonardo da Vinci, Albrescht Dürer, Salvador Dali, dentre outros e também, em muitas obras da arquitetura clássica em que temos como exemplo claro o Pathernon.
Da Vinci
Leonardo da Vinci usou Phi para pintar a Mona Lisa, uma de suas mais notáveis obras. Em vários pontos da obra, tais como nas relações entre seu tronco e cabeça, ou entre os elementos do rosto aparece a razão áurea.

Outra obra de Da Vinci em que se vê com bastante clareza o uso da Razão Áurea é o Homem Vitruviano como nota-se na imagem a seguir.

Pathernon

Retângulo áureo no Parthenon
Na imagem abaixo, o frontispício dessa obra, hoje em ruínas, está sobreposta por formas retangulares.

Se dividirmos as medidas dos lados maiores pelas medidas dos lados menores desses retângulos, obteremos números próximos da razão a "phi" = 1,618034...
Chamamos de retângulo áureo aquele em que se aplica a seguinte propriedade: de um retângulo ABCD, suprimimos um quadrado ABEF, restando assim, um novo retângulo CDEF, sendo que, se este for semelhante ao original, então ABCD é áureo.
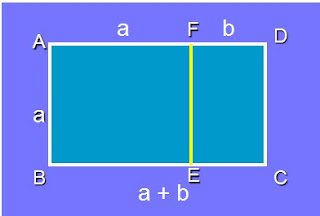
Assim, podemos traduzir a definição acima da seguinte maneira:
a/a+b = b/a (1)
Da relação (1) decorre, a seguinte propriedade das proporções, onde:

Isto significa que se o retângulo de lados a + b e a é áureo, logo o retângulo de lados a e b também será áureo e assim, sucessivamente.

Outras Aplicações
Ainda hoje há artistas usando a “divina proporção” em seus trabalhos, e cientistas, como Roger Penrose, estão descobrindo muitas aplicações da razão áurea na matemática e na natureza.
Sabe-se hoje que existe uma ligação entre a razão áurea e a série de Fibonacci. A seqüência 1, 1, 2, 3, 5, 8, 13, ..., correspondente aos lados dos quadrados que montam essa espiral, é a mesma que Leonardo Pisano (Fibonacci 1180-1250), em seu livro Liber Abbaci, de 1202, calculou para o crescimento das populações de coelhos a partir de um casal.
Dividindo, a partir do terceiro termo dessa seqüência, o número deste termo pelo número do termo anterior, teremos a seqüência de frações 1/1, 2/1, 3/2, 5/3, 8/5, 13/8, 21/13... que se aproximará cada vez mais da razão áurea fhi = 1,618034...
Observe a figura abaixo:

Assim, podemos perceber que razão entre os termos consecutivos da seqüência de Fibonacci tendem a phi.
A razão áurea e a seqüência de Fibonacci
Agrupados na forma vista na figura anterior, temos uma seqüência de quadrados com lados de medidas iguais aos números da seqüência de Fibonacci (1, 1, 2, 3, 5, 8, 13, 21...) e assim, se formará uma espiral muito encontrada em formas da natureza, a chamada Espiral de conchas e flores.

Esta espiral pode ser vista facilmente no molusco náutilo (Nautilus pompilius) e na distribuição de pétalas de diversas flores.

Observe na figura a seguir como realmente pode-se encontrar uma seqüência de retângulo de ouro formando a espiral de fibonacci.

TRIÂNGULO DE OURO
Um triângulo é um triângulo áureo quando ele é semelhante ao triângulo retângulo com hipotenusa medindo 1,618... (phi) e catetos com medidas 1 e 1,272... (raiz quadrada de phi). Assim, um triângulo retângulo com hipotenusa a e catetos b e c (b > c) é áureo se, e somente se,

Acredita-se que, no Egito, as pirâmides de Gizé foram construídas tendo em conta a razão áurea. A razão entre a altura de um face e metade do lado da base da grande pirâmide é igual ao número de ouro. O Papiro de Rhind (Egípcio) refere-se a uma “razão sagrada” que se crê ser o número de ouro. Esta razão ou secção áurea surge em muitas estátuas da antiguidade. A razão aparece, também, na proporção entre altura e lados e nas câmaras internas.


Logo, para verificarmos se uma pirâmide é ou não áurea, devemos analisar a seguinte definição:
Pirâmide reta de altura h com base quadrada de lado a e a altura de suas faces seja H. Desta maneira, quando o triângulo de lados H, h e a/2 for um triângulo áureo, a pirâmide também será áurea.
De acordo com a definição, tem-se:

Demonstração:
Uma pirâmide áurea, isto é, em que o triângulo retângulo com hipotenusa e catetos h e a/2, (supondo h > a/2) é áureo.
Temos então:

E portanto,

Analogamente, das relações, temos:

obtemos

que implica

que resulta

Logo,

e, portanto, o triângulo de lados H, h e a/2.
Dentre os polígonos de ouro estão o triângulo, o retângulo.
RETÂNGULO DE OURO
Os retângulos áureos estão nas obras gregas, nas obras de Leonardo da Vinci, Albrescht Dürer, Salvador Dali, dentre outros e também, em muitas obras da arquitetura clássica em que temos como exemplo claro o Pathernon.
Da Vinci
Leonardo da Vinci usou Phi para pintar a Mona Lisa, uma de suas mais notáveis obras. Em vários pontos da obra, tais como nas relações entre seu tronco e cabeça, ou entre os elementos do rosto aparece a razão áurea.

Outra obra de Da Vinci em que se vê com bastante clareza o uso da Razão Áurea é o Homem Vitruviano como nota-se na imagem a seguir.

Pathernon

Retângulo áureo no Parthenon
Na imagem abaixo, o frontispício dessa obra, hoje em ruínas, está sobreposta por formas retangulares.

Se dividirmos as medidas dos lados maiores pelas medidas dos lados menores desses retângulos, obteremos números próximos da razão a "phi" = 1,618034...
Chamamos de retângulo áureo aquele em que se aplica a seguinte propriedade: de um retângulo ABCD, suprimimos um quadrado ABEF, restando assim, um novo retângulo CDEF, sendo que, se este for semelhante ao original, então ABCD é áureo.

Assim, podemos traduzir a definição acima da seguinte maneira:
a/a+b = b/a (1)
Da relação (1) decorre, a seguinte propriedade das proporções, onde:

Isto significa que se o retângulo de lados a + b e a é áureo, logo o retângulo de lados a e b também será áureo e assim, sucessivamente.

Outras Aplicações
Ainda hoje há artistas usando a “divina proporção” em seus trabalhos, e cientistas, como Roger Penrose, estão descobrindo muitas aplicações da razão áurea na matemática e na natureza.
Sabe-se hoje que existe uma ligação entre a razão áurea e a série de Fibonacci. A seqüência 1, 1, 2, 3, 5, 8, 13, ..., correspondente aos lados dos quadrados que montam essa espiral, é a mesma que Leonardo Pisano (Fibonacci 1180-1250), em seu livro Liber Abbaci, de 1202, calculou para o crescimento das populações de coelhos a partir de um casal.
Dividindo, a partir do terceiro termo dessa seqüência, o número deste termo pelo número do termo anterior, teremos a seqüência de frações 1/1, 2/1, 3/2, 5/3, 8/5, 13/8, 21/13... que se aproximará cada vez mais da razão áurea fhi = 1,618034...
Observe a figura abaixo:

Assim, podemos perceber que razão entre os termos consecutivos da seqüência de Fibonacci tendem a phi.
A razão áurea e a seqüência de Fibonacci
Agrupados na forma vista na figura anterior, temos uma seqüência de quadrados com lados de medidas iguais aos números da seqüência de Fibonacci (1, 1, 2, 3, 5, 8, 13, 21...) e assim, se formará uma espiral muito encontrada em formas da natureza, a chamada Espiral de conchas e flores.

Esta espiral pode ser vista facilmente no molusco náutilo (Nautilus pompilius) e na distribuição de pétalas de diversas flores.

Observe na figura a seguir como realmente pode-se encontrar uma seqüência de retângulo de ouro formando a espiral de fibonacci.

TRIÂNGULO DE OURO
Um triângulo é um triângulo áureo quando ele é semelhante ao triângulo retângulo com hipotenusa medindo 1,618... (phi) e catetos com medidas 1 e 1,272... (raiz quadrada de phi). Assim, um triângulo retângulo com hipotenusa a e catetos b e c (b > c) é áureo se, e somente se,

Acredita-se que, no Egito, as pirâmides de Gizé foram construídas tendo em conta a razão áurea. A razão entre a altura de um face e metade do lado da base da grande pirâmide é igual ao número de ouro. O Papiro de Rhind (Egípcio) refere-se a uma “razão sagrada” que se crê ser o número de ouro. Esta razão ou secção áurea surge em muitas estátuas da antiguidade. A razão aparece, também, na proporção entre altura e lados e nas câmaras internas.


Logo, para verificarmos se uma pirâmide é ou não áurea, devemos analisar a seguinte definição:
Pirâmide reta de altura h com base quadrada de lado a e a altura de suas faces seja H. Desta maneira, quando o triângulo de lados H, h e a/2 for um triângulo áureo, a pirâmide também será áurea.
De acordo com a definição, tem-se:

Demonstração:
Uma pirâmide áurea, isto é, em que o triângulo retângulo com hipotenusa e catetos h e a/2, (supondo h > a/2) é áureo.
Temos então:

E portanto,

Analogamente, das relações, temos:

obtemos

que implica

que resulta

Logo,

e, portanto, o triângulo de lados H, h e a/2.
domingo, 21 de fevereiro de 2010
É possível avaliar a beleza física de uma pessoa por meio de uma fórmula matemática?
A beleza é subjetiva! O que é belo para uma pessoa pode não ser para outra. Porém, é possível mostrar a harmonia de suas proporções, realizando comparações. No processo de comparação é necessário um critério especial, denominado medida.
Qual é essa medida? É uma razão?
Vamos tomar um segmento AB, tal que a med (AB) = x unidade. É como se este segmento fosse, por exemplo, a medida da altura de uma pessoa.

Com um ponto C podemos dividir este segmento em duas partes.
De quantas maneiras podemos dividir este segmento?
Observamos que o ponto C pode ocupar infinitas posições, mas existe uma única posição - posição de ouro – onde este ponto C divide o segmento AB em dois segmentos proporcionais, tal que, o quociente entre as medidas do segmento todo pela parte maior é igual ao quociente entre as medidas da parte maior com a parte menor:

No exemplo dado, a posição ouro do ponto C é obtida da seguinte forma:

Sendo a medida (AB) = x, a med(AC) = a e med(CB) = (x- a), então:

A propriedade fundamental da proporção nos garante que: x.(x – a) = a2 , aplicando a propriedade distributiva, temos a equação do 2º grau:

Resolvendo a equação, temos:

Portanto o número é um número irracional, denominado número de ouro. Ou seja,

e a razão inversa do número de ouro

Como a é a medida do segmento maior AC, temos que a = x.(0,6180399...) é denominada secção áurea do segmento AB.
O número de ouro é considerado especial por ter propriedades interessantes, como:
P1: Somando 1 ao número de ouro obtém-se o seu quadrado:

( 1 + 1,6180399....) = ( 1,618...) 2 = 2,6180399....
P2: Subtraindo 1 de phi, obtém-se o seu inverno:

Agora que já conhecemos qual é essa razão, vamos responder a pergunta inicial.
Façamos um teste tomando as respectivas medidas: altura (ou medida do corpo) e medida da linha umbilical até o chão e, em seguida, fazendo as seguintes divisões: altura (x) pela medida do umbigo ao chão (a) e vice-versa.
Encontrou alguma coincidência de resultados?

Será que somos bonitos? Ou melhor, será que nossas proporções são harmônicas?
Qual a importância do salto alto? Todas as mulheres deveriam usar salto alto?
De acordo com as definições e propriedades vistas, que tal verificarmos a harmonia das proporções do nosso corpo?
Será que pessoas consideradas exemplo de beleza, como a top model Gisele Bündchen possuem proporções harmônicas?
Tente! Vai ser muito interessante.
Selecione algumas das fotografias de pessoas consideradas como referencial de beleza. Agora, de acordo com as propriedades das proporções áureas , verifique se essas pessoas podem ser consideradas “belas”, ou seja, se as suas medidas são harmônicas.
A partir desta discussão, você concorda ou não que a beleza está intrinsecamente relacionada à matemática, ou seja, ao número de ouro? Dê sua opinião.
Qual é essa medida? É uma razão?
Vamos tomar um segmento AB, tal que a med (AB) = x unidade. É como se este segmento fosse, por exemplo, a medida da altura de uma pessoa.

Com um ponto C podemos dividir este segmento em duas partes.
De quantas maneiras podemos dividir este segmento?
Observamos que o ponto C pode ocupar infinitas posições, mas existe uma única posição - posição de ouro – onde este ponto C divide o segmento AB em dois segmentos proporcionais, tal que, o quociente entre as medidas do segmento todo pela parte maior é igual ao quociente entre as medidas da parte maior com a parte menor:

No exemplo dado, a posição ouro do ponto C é obtida da seguinte forma:

Sendo a medida (AB) = x, a med(AC) = a e med(CB) = (x- a), então:

A propriedade fundamental da proporção nos garante que: x.(x – a) = a2 , aplicando a propriedade distributiva, temos a equação do 2º grau:

Resolvendo a equação, temos:

Portanto o número é um número irracional, denominado número de ouro. Ou seja,

e a razão inversa do número de ouro

Como a é a medida do segmento maior AC, temos que a = x.(0,6180399...) é denominada secção áurea do segmento AB.
O número de ouro é considerado especial por ter propriedades interessantes, como:
P1: Somando 1 ao número de ouro obtém-se o seu quadrado:

( 1 + 1,6180399....) = ( 1,618...) 2 = 2,6180399....
P2: Subtraindo 1 de phi, obtém-se o seu inverno:

Agora que já conhecemos qual é essa razão, vamos responder a pergunta inicial.
Façamos um teste tomando as respectivas medidas: altura (ou medida do corpo) e medida da linha umbilical até o chão e, em seguida, fazendo as seguintes divisões: altura (x) pela medida do umbigo ao chão (a) e vice-versa.
Encontrou alguma coincidência de resultados?

Será que somos bonitos? Ou melhor, será que nossas proporções são harmônicas?
Qual a importância do salto alto? Todas as mulheres deveriam usar salto alto?
De acordo com as definições e propriedades vistas, que tal verificarmos a harmonia das proporções do nosso corpo?
Será que pessoas consideradas exemplo de beleza, como a top model Gisele Bündchen possuem proporções harmônicas?
Tente! Vai ser muito interessante.
Selecione algumas das fotografias de pessoas consideradas como referencial de beleza. Agora, de acordo com as propriedades das proporções áureas , verifique se essas pessoas podem ser consideradas “belas”, ou seja, se as suas medidas são harmônicas.
A partir desta discussão, você concorda ou não que a beleza está intrinsecamente relacionada à matemática, ou seja, ao número de ouro? Dê sua opinião.
O Número de Ouro e a Razão Áurea
No texto anterior, vimos uma série situações da natureza e obras criadas por vários povos com culturas distintas, cuja foco se baseia sempre na procura pelo belo, por proporções que as tornem mais belas e harmoniosas aos nossos olhos.
Mas o que torna isso possível? Que relação matemática é capaz de proporcionar tal sensação de harmonia e beleza? O que há de comum em situações tão diferentes como uma pintura renascentista e obras da arquitetura da Antiguidade Clássica, ou então situações que envolvam a natureza, como a relação entre o crescimento de uma determinada população e um molusco (Náutilus Pompilius)? Será possível avaliar a beleza física de uma pessoa por meio de uma fórmula matemática? E qual a relação entre as pétalas de um girassol e uma figura geométrica como o Pentágono de ouro (traçando-se suas diagonais forma-se o Pentagrama).?
A resposta destas perguntas é a mesma, e pode parecer algo meio ilógico ou um tanto quanto irreal, imaginário, mas, existe e é uma resposta matemática. Trata-se do Número de Ouro
(phi) recebendo este nome em homenagem ao grande arquiteto e escultor grego chamado Phidias. Por isso, o nome de Phi para esta letra que representa “Número de Ouro”.
Entretanto, não se tem registros de quem iniciou os estudos sobre esse misterioso número, mas a primeira definição clara que se tem sobre essa intrigante proporção, aparece no livro Elementos de Euclides. Contudo, acredita-se que Euclides tenha se baseado em estudos de matemáticos anteriores a ele como Pitágoras e Theodoro de Cyrene. Todavia, foi através dos Elementos, mais especificamente nos livros II, IV, VI e XIII (Elementos era composto por 13 Livros), que a Razão Áurea ficou amplamente conhecida, sendo, Elementos, o livro mais vendido (após a Bíblia) até o século XX.
O número de Ouro e a proporção a ele associada, também foi estudada pelo monge italiano Luca Pacioli, de Veneza, no livro De Divina Proportione (Sobre a proporção divina), de 1509 que a denominou "Divina Proporção". Assim, sendo conhecido desde a antiguidade, o Número de Ouro recebeu inúmeras denominações além das já citadas, como Número Áureo, Secção Áurea e por fim Razão Áurea.
Mas como determinar este número? Seria ele dado através do ponto médio de um segmento? O resultado dessa misteriosa divisão, simbolizado pela letra grega (lê-se "fi") é sempre 1,618034... ou (1+√5)/2, ficando amplamente conhecido como razão áurea. A seguir, veremos um processo matemático para determinarmos este fascinante número.
Mas o que torna isso possível? Que relação matemática é capaz de proporcionar tal sensação de harmonia e beleza? O que há de comum em situações tão diferentes como uma pintura renascentista e obras da arquitetura da Antiguidade Clássica, ou então situações que envolvam a natureza, como a relação entre o crescimento de uma determinada população e um molusco (Náutilus Pompilius)? Será possível avaliar a beleza física de uma pessoa por meio de uma fórmula matemática? E qual a relação entre as pétalas de um girassol e uma figura geométrica como o Pentágono de ouro (traçando-se suas diagonais forma-se o Pentagrama).?
A resposta destas perguntas é a mesma, e pode parecer algo meio ilógico ou um tanto quanto irreal, imaginário, mas, existe e é uma resposta matemática. Trata-se do Número de Ouro
(phi) recebendo este nome em homenagem ao grande arquiteto e escultor grego chamado Phidias. Por isso, o nome de Phi para esta letra que representa “Número de Ouro”.
Entretanto, não se tem registros de quem iniciou os estudos sobre esse misterioso número, mas a primeira definição clara que se tem sobre essa intrigante proporção, aparece no livro Elementos de Euclides. Contudo, acredita-se que Euclides tenha se baseado em estudos de matemáticos anteriores a ele como Pitágoras e Theodoro de Cyrene. Todavia, foi através dos Elementos, mais especificamente nos livros II, IV, VI e XIII (Elementos era composto por 13 Livros), que a Razão Áurea ficou amplamente conhecida, sendo, Elementos, o livro mais vendido (após a Bíblia) até o século XX.
O número de Ouro e a proporção a ele associada, também foi estudada pelo monge italiano Luca Pacioli, de Veneza, no livro De Divina Proportione (Sobre a proporção divina), de 1509 que a denominou "Divina Proporção". Assim, sendo conhecido desde a antiguidade, o Número de Ouro recebeu inúmeras denominações além das já citadas, como Número Áureo, Secção Áurea e por fim Razão Áurea.
Mas como determinar este número? Seria ele dado através do ponto médio de um segmento? O resultado dessa misteriosa divisão, simbolizado pela letra grega (lê-se "fi") é sempre 1,618034... ou (1+√5)/2, ficando amplamente conhecido como razão áurea. A seguir, veremos um processo matemático para determinarmos este fascinante número.
A FASCINANTE RAZÃO ÁUREA
"A Geometria possui dois grandes tesouros: um é o teorema de Pitágoras; o outro a Proporção áurea." (Kepler)
“Na origem, na gênese universal, Deus ao criar os ‘moldes’ para a geração do universo, sem dúvida, teve como um desses moldes divinos um número. Mas não um número qualquer, mas sim, um número especial, um número que estivesse presente na massa ‘informe’ e colossal do universo em criação. Este número cósmico e ao mesmo tempo mítico, está presente em diversos corpos e fenômenos da natureza, formando uma espécie de ‘DNA’ universal, sendo encontrado em conchas de moluscos, pétalas de girassóis, gomos de abacaxis, no corpo humano, nos chifres de cordeiros selvagens..., e até nos confins do universo.”
RAZÃO ÁUREA
A preocupação com a beleza, física ou do meio não é recente. A todo momento, fazemos julgamentos estéticos. Isto já vem dos nossos ancestrais. Acreditamos que desde os tempos primitivos o ser humano tem permanecido em “ estado de indagação ” sobre a harmonia e a beleza do universo. Mas quais os critérios que nos baseamos para realizarmos nossas avaliações?
Na tentativa de justificar o belo, definir a beleza, o homem procurou estabelecer uma ordem de comparação entre os objetos que o rodeiam. A Matemática guarda uma relação estreita com o belo, com o esteticamente agradável, que por muitas ocasiões aflora em seus mais variados temas.
Durante séculos, especialmente na Grécia Antiga, a beleza foi um conceito intimamente ligado à Geometria. Platão acreditava que o belo residia no tamanho apropriado das partes, que ajustavam-se de forma harmônica no todo, em equilíbrio.
Muitos acreditavam que a personificação desse ideal seria Helena de Tróia, que por possuir uma beleza tão deslumbrante, foi elevada à categoria de semideusa. No Egito, tinha-se como referencial de beleza a rainha Nefertiti, esposa do faraó Amenófis IV, que possuía um semblante perfeitamente simétrico e perfil bem delineado.

Obras da arquitetura clássica, como o Parthenon, revelam o uso da razão áurea na busca de uma harmonia estética.

Durante a Idade Média, muitas Catedrais foram construídas utilizando equações matemáticas em seus projetos arquitetônicos, afim de que suas proporções fossem perfeitas, ou seja, elas fossem mais belas.

(Catedral de Notre Dame, Paris)
Com o advento da Renascença (fim da Idade Média e início da Idade Moderna), pintores renascentistas como Leonardo da Vinci, Michelangelo, Albrecht Dürer entre outros, passaram a utilizar em suas obras o conceito da proporção áurea.
Atualmente com sua principal propriedade, a autopropagação, as secções áureas ultrapassam os limites da arte e da arquitetura, tendo aplicações em diversas áreas do conhecimento.
“Na origem, na gênese universal, Deus ao criar os ‘moldes’ para a geração do universo, sem dúvida, teve como um desses moldes divinos um número. Mas não um número qualquer, mas sim, um número especial, um número que estivesse presente na massa ‘informe’ e colossal do universo em criação. Este número cósmico e ao mesmo tempo mítico, está presente em diversos corpos e fenômenos da natureza, formando uma espécie de ‘DNA’ universal, sendo encontrado em conchas de moluscos, pétalas de girassóis, gomos de abacaxis, no corpo humano, nos chifres de cordeiros selvagens..., e até nos confins do universo.”
RAZÃO ÁUREA
A preocupação com a beleza, física ou do meio não é recente. A todo momento, fazemos julgamentos estéticos. Isto já vem dos nossos ancestrais. Acreditamos que desde os tempos primitivos o ser humano tem permanecido em “ estado de indagação ” sobre a harmonia e a beleza do universo. Mas quais os critérios que nos baseamos para realizarmos nossas avaliações?
Na tentativa de justificar o belo, definir a beleza, o homem procurou estabelecer uma ordem de comparação entre os objetos que o rodeiam. A Matemática guarda uma relação estreita com o belo, com o esteticamente agradável, que por muitas ocasiões aflora em seus mais variados temas.
Durante séculos, especialmente na Grécia Antiga, a beleza foi um conceito intimamente ligado à Geometria. Platão acreditava que o belo residia no tamanho apropriado das partes, que ajustavam-se de forma harmônica no todo, em equilíbrio.
Muitos acreditavam que a personificação desse ideal seria Helena de Tróia, que por possuir uma beleza tão deslumbrante, foi elevada à categoria de semideusa. No Egito, tinha-se como referencial de beleza a rainha Nefertiti, esposa do faraó Amenófis IV, que possuía um semblante perfeitamente simétrico e perfil bem delineado.

Obras da arquitetura clássica, como o Parthenon, revelam o uso da razão áurea na busca de uma harmonia estética.

Durante a Idade Média, muitas Catedrais foram construídas utilizando equações matemáticas em seus projetos arquitetônicos, afim de que suas proporções fossem perfeitas, ou seja, elas fossem mais belas.

(Catedral de Notre Dame, Paris)
Com o advento da Renascença (fim da Idade Média e início da Idade Moderna), pintores renascentistas como Leonardo da Vinci, Michelangelo, Albrecht Dürer entre outros, passaram a utilizar em suas obras o conceito da proporção áurea.
Atualmente com sua principal propriedade, a autopropagação, as secções áureas ultrapassam os limites da arte e da arquitetura, tendo aplicações em diversas áreas do conhecimento.
Assinar:
Postagens (Atom)